Sorting Complicated Knots
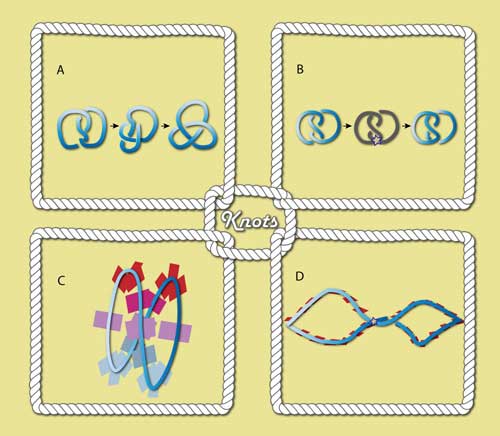
From bow ties and shoelaces to sailing boats and climbing ropes, knots are not only very useful for our daily lives, but for mathematics too. IBS researchers from the Center for Geometry and Physics, within the Institute for Basic Science (IBS) reported a new mathematical operation to catalog a special kind of mathematical knots, known […]
